# CPU缓存模型
一般来说,CPU不会直接从内存中读取数据,会按L1(线程本地缓存) -> L2(线程本地缓存) -> L3(线程共享缓存)的缓存顺序,先去CPU的缓存中查询是否有指定变量。如果没有,才会去主存中读取数据。下图是我整理的MAC的缓存模型,和一般的处理器有一些不一样,只有L2和L3级缓存,并没有L1级缓存,不过这并不影响我们学习。
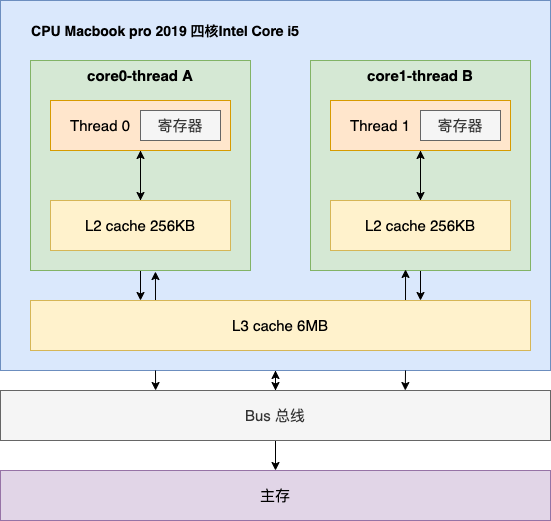
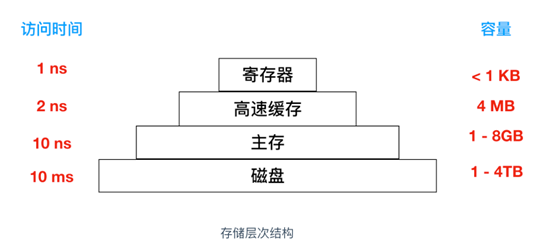
至于为什么会按照这个顺序去读取变量呢,我们可以看另外一张图。从这张图我们就能明显看到读取速度的差异,其中从寄存器中读取变量,和从磁盘中读取变量,速度可以相差1000万倍。所以,越靠近CPU核心,速度就越快。
这里会引申出一个问题,为什么CPU高速缓存这么快,L2才256KB, L3才6MB,加起来也不到10MB? 这是因为CPU这个元件本身很小,工艺非常复杂。如果要加更多的内存进去,成本非常高,所以也可以理解为在这中间做了一个取舍。
说到CPU的缓存模型,就必然会提到两个点,时间局部性和空间局部性
# 时间局部性
CPU认为,如果一个变量被使用,那么它会快会再次被使用。所以在一个变量使用完之后,不会立即被丢弃。而是在一段时间后才会失效。
# 空间局部性
CPU认为,如果一个变量被使用,那么它的临近变量也会很快被使用。所以当CPU从主存中读取一个变量的时候,也会同时将这个变量的临近变量一起读取到缓存中。
下面我们用一个例子来证明CPU的空间局部性
# 证明逻辑
初始化一个数组,数组大小是[1024 * 1024][64],也就是初始化一个64列,1024*1024行的数组
将数组的的全部位置初始化为1,然后对数组进行求和
第一种方式是行优先加,也就是先将一行累加结束,再累加第二行
第二种方式是列优先加,也就是先将一列累加结束,再累加第二列
假设:按照空间局部性原则,一行数组的地址连续,在读取第一行的时候,就会将这一行所有的数据加载到缓存中,一行也就只会读取一次缓存,也按列加的话,每次读取一个数据,都需要从内存中去加载。按照这个假设,我们可以得出以下结论。
- 按行加读取内存次数:1024 * 1024,也就是行数
- 按列加读取内存次数:1024 * 1024 * 64,所有元素的总数
在证明之前,我们先看一张图,了解一下数组在内存中是如何存储的。可以看到,每行的数据在内存中地址是连续的,而列并不连续。
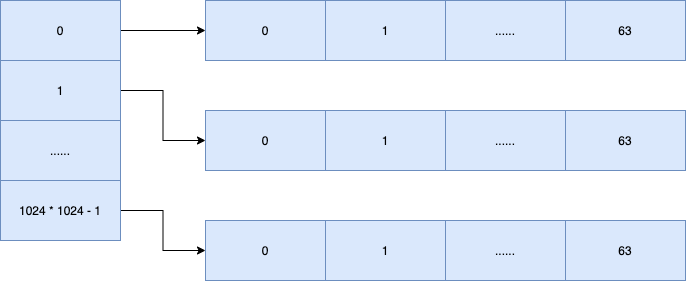
代码证明
public class SpacePartTest {
/**
* 测试空间局部性
*
* cpu在读取一个变量的时候,如果在内部缓存读取不到,会直接读取内存。
* 但cpu认为,如果一个变量被使用到,那么它临近的变量也会很快被使用到
* 所以cpu在读取一个变量的同时,也会读取这个变量的临近变量
*
* 下面是一个测试,初始化一个行数为1024 * 1024,列数为64的数组,将数组的全部值初始化为1
* 我们来测试一个结论,按行加,使用到空间局部性,速度会快于按列加
*
*
* @param args
*/
public static void main(String[] args) {
int xLen = 64;
int yLen = 1024 * 1024;
int[][] nums = new int[yLen][xLen];
for (int y = 0; y < yLen; y++) {
for (int x = 0; x < xLen; x++) {
nums[y][x] = 1;
}
}
int sum = 0;
StopWatch stopWatch = new StopWatch();
stopWatch.start("行优先加");
for (int y = 0; y < yLen; y++) {
for (int x = 0; x < xLen; x++) {
sum += nums[y][x];
}
}
stopWatch.stop();
stopWatch.start("列优先加");
sum = 0;
for (int x = 0; x < xLen; x++) {
for (int y = 0; y < yLen; y++) {
sum += nums[y][x];
}
}
stopWatch.stop();
System.out.println(stopWatch.prettyPrint());
}
}
- 测试结果,从结果中我们可以明显的看到,按列加占据了绝大部分的时间。
StopWatch '': running time = 1265081620 ns
---------------------------------------------
ns % Task name
---------------------------------------------
076201035 006% 行优先加
1188880585 094% 列优先加
- 结论:假设正确