学习才是源动力

# 索引的数据结构与算法

# 带着问题去听

  1. 为什么要有索引？
  2. 索引常见的数据结构有哪些？
  3. 为什么会存在二叉树 -> 红黑树 -> B树 -> B+树这么一个演进过程？
  4. B+树和B树的区别是什么，为什么是B+树而不是B树？
  5. 我们常说，MySQL是支撑千万级数据量的数据库，在千万级的数据量下也能实现快速返回结果，这是怎么做到的？

# 为什么要有索引

我们来想象一个场景：假如你有一本新华字典，乱序的，像错版人民币一样，孤本，价值很高。但当你拿着这本字典需要去查询一个字的时候，你会怎么办？

  1. 你想，没关系，价值大于时间，而且也不是不能用，大不了就是一页一页的翻。好一点的情况是，你从前几页找到了想要的字，而坏一点的情况是，你翻到最后一页才翻到。从算法的角度来说，这一次查询就是o(n)的时间复杂度。 在数据量少，比如只有几十页的情况下，一页一页的翻，也没关系。那么，如果数据量大呢，几十万，几百万，上千万呢，一页一页的翻到天荒地老？
  2. 这个时候，你想到了一个办法，内容无序是吧，我建一个目录，目录我取字的拼音，按a,b,c的顺序进行排序，那只要维护好这个有序的目录，我是不是可以快速的通过拼音定位，就能把字找到了。

图片0

其实，为什么举这个例子呢？我们可以想一下，比如一个全国的用户信息表，不对某些字段进行排序，任由数据野蛮增长，那数据对我们而言，可不就是乱序的吗？

# 索引的本质

索引本质是帮助数据库高效获取数据的排好序的数据结构

以这张图为例

图片1

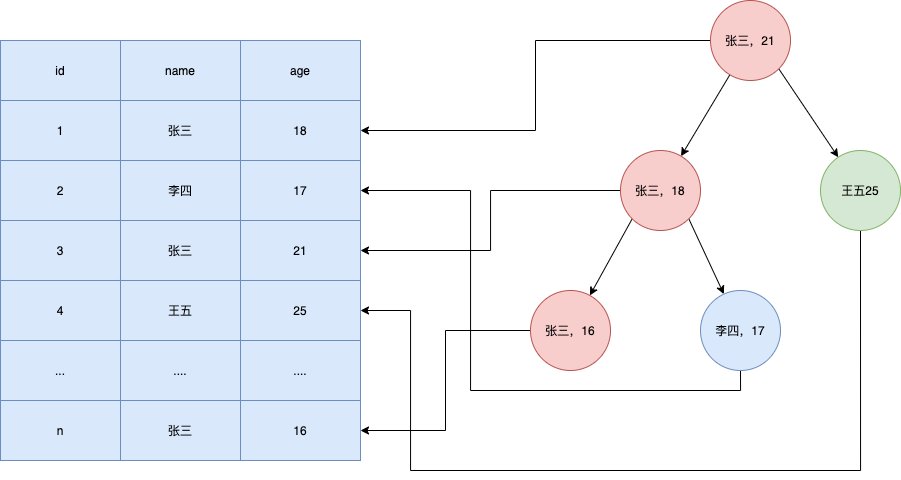
如果我们有一条SQL如下

select * from t where name = '张三';

在没有索引的时候，需要一行一行的去扫。就算找到第一个张三，也不能确保后面没有张三，所以需要扫描完所有的数据。

你可能会说了，数据看起来是连续存储的，就算扫描完所有的数据，应该也很快，不会花太多的时间。

这里我们要理解一个概念，select查出来的，看起来是连续的数据，不一定是存在同一个盘上

# 为什么看起来相邻的记录，实际上存储的地址不连续？

我们想象磁盘写数据的一个过程，首先第一条数据来了, 在磁盘空间A未被占满的情况下，把数据放在磁盘位置A。然后第二条数据来了，磁盘空间A可能已经被占满了, 那就只能往后放了，可能是B，也可能是E。 也就是说，看起来相邻的记录，在磁盘上的存放是分散的，不连续的。我们都知道，一次磁盘文件读取，就是一次文件IO，而文件IO的效率是不高的。如果表记录很多，逐行逐行的去读取，不断的进行IO操作，查询效率肯定是很低下的。

图片2

# 一个结论

由此，我们找到了性能瓶颈，得出了一个结论：文件IO次数与我们的查询时间成正比，文件IO次数越多，查询时间越长。如果我们想要加快查询速度，就需要把文件IO次数控制在一定范围内。

# 二叉树，红黑树，Hash，B树，B+树详解

# 二叉树

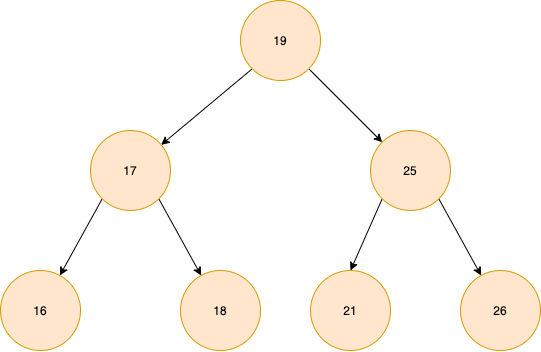
以下面这个图为例，我们基于filed1构建索引，key为索引字段的值，value为索引所在行的磁盘文件地址。

二叉树的查询一般从根节点开始，父元素右边的元素大于父元素，左边的值小于父元素。如果我们查询filed1=26的数据，只需要经过三次查询，就能定位文件所在行，三次文件IO即可取出数据。 比单纯的逐行查询效率要高。查询次数取决于树的高度，时间复杂度O(log(n)) 图片3

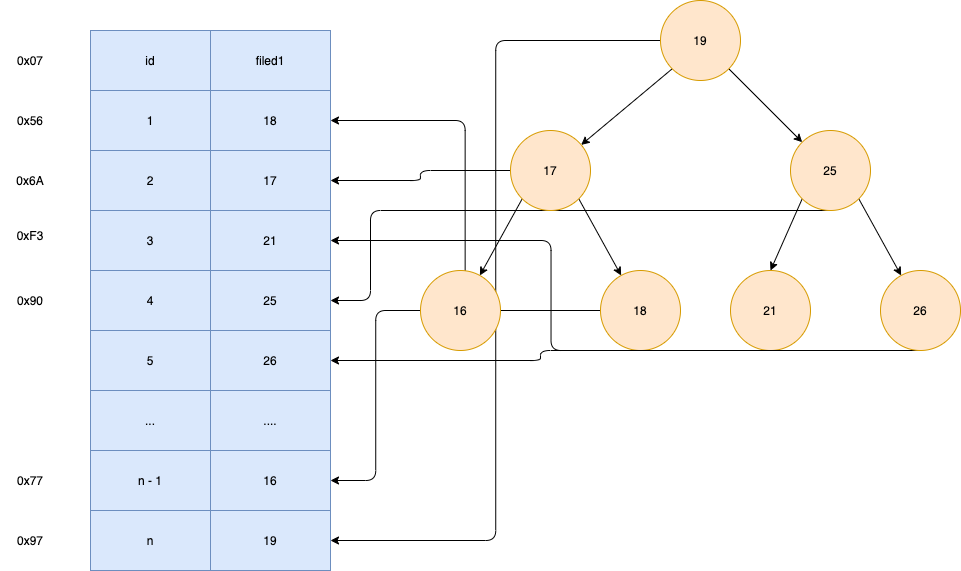
但实际上，MySQL并没有使用二叉树作为索引结构，为什么呢？我们看id列，其实是有序自增数字。而每次有数据新增的时候，二叉树会按照规则进行插入：即右子节点大于父节点。

简单实验一下：二叉树图解 (opens new window) 图片4

看实验结果我们会发现，在这种情况下二叉树退化成链表了。退化之后，需要逐个扫描索引，才能取到我们想要数据。 还是O(n)的时间复杂度，效率根本就没有提升。所以对于这种单边增长的列，使用二叉树根本没有什么优化，这也就是MySQL并没有使用二叉树的原因了。

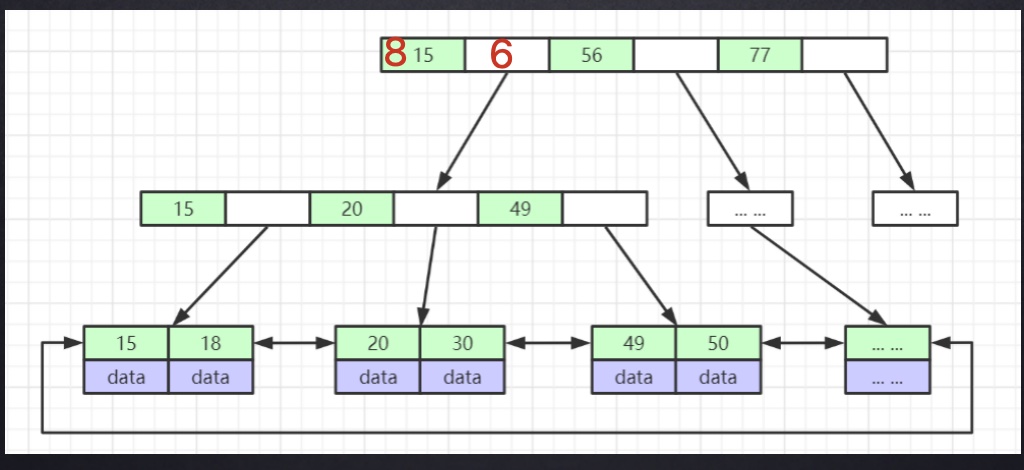
# 红黑树

有人可能会说了，从java8开始，HashMap引入了红黑树，从之前的数组+链表的结构改成了数组+链表/红黑树的结构。那用红黑树可以吗？我们来看一下红黑树的结构

简单实验一下：红黑树图解 (opens new window)

图片5

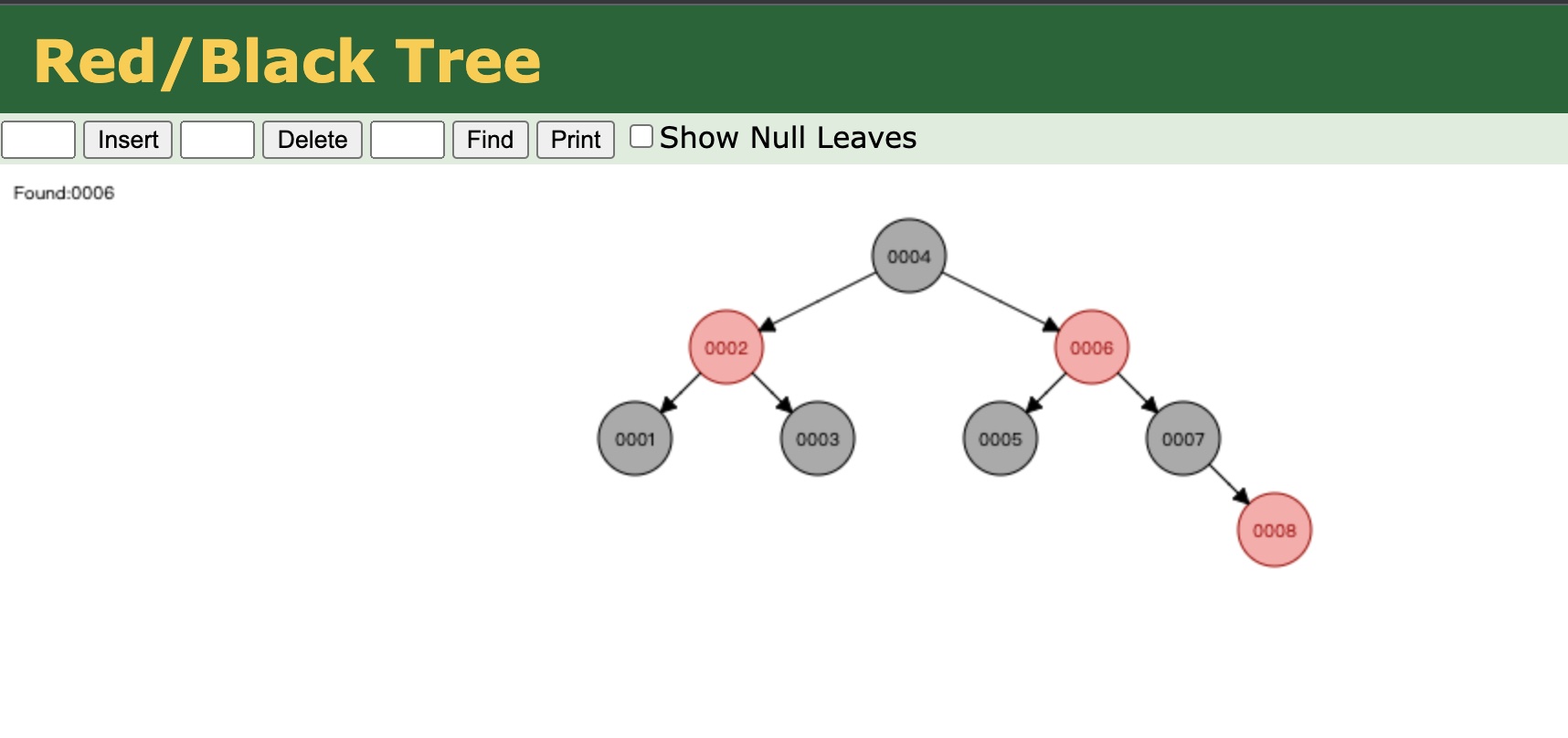
从实验中我们可以看到，红黑树在插入的过程中会进行平衡。平衡之后，我们再查找6，只需要两次查询就可以拿到结果。也就是说，红黑树在二叉树的结构上进行了优化，是一棵平衡的二叉树，但是MySQL依然没有使用红黑树。

为什么呢？因为红黑树是一棵平衡二叉树，说白了，也是一棵二叉树，假如有500万行的数据，那么树的高度是多少是不是会很高。

我们可以简单计算一下，像下图这样，按最优的情况去计算，即每个叶子节点都被撑满的情况。 图片5

公式推导：

2^1 - 1 = 1；
2^2 - 1 = 2;
2^3 - 1 = 7;

设高度为n，我们可以得出以下公式
2^n - 1 = 500w
n = log2(5000001)

图片6 在最理想的情况下，树的高度大概是22。

  1. 如果要查询的数据在叶子节点，也就是说我们需要22次的文件IO才能查询到数据，效率其实还是没有得到太大的提升
  2. 而且在数据量持续增长的情况下，树的高度不可控

# 另一个结论

从这里我们可以得出一个新的结论，查询次数也就是文件IO次数和树的高度成正比，树的高度越高，查询次数越多。只要我们降低树的高度，将树的高度控制下来，降低文件IO次数，就能优化查询速度。

接下来我们的目标是对红黑树做一点改造，希望树的高度固定，一个节点横向存放存放更多的数据。

# B树

  • 叶节点具有相同的深度，叶节点的指针为空
  • 所有索引元素不重复
  • 节点中的数据索引从左到右递增排列

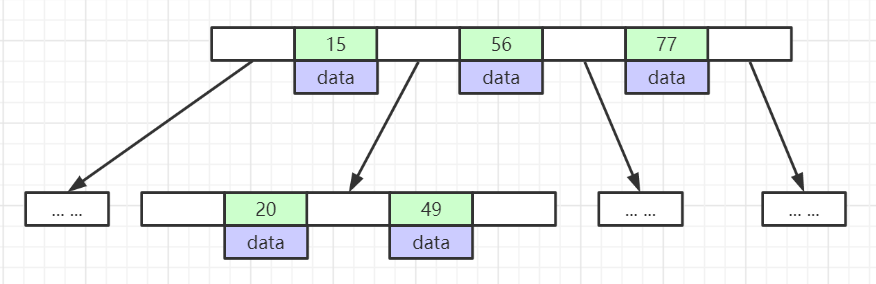
B-Tree

但事实是，MySQL也没有用纯粹B树作为索引的数据结构，而是对B树做了一点优化改造，得到了另外一种数据结构: B+树

# B+树

  • 非叶子节点不再存储data，只存储索引(冗余，以每一个磁盘页的开始节点为父节点，构建B+树)，可以放更多的索引
  • 节点中的数据索引从左到右递增排列 【与B树相同】
  • 叶子节点包含所有索引字段
  • 叶子节点用指针连接，提高区间访问的性能

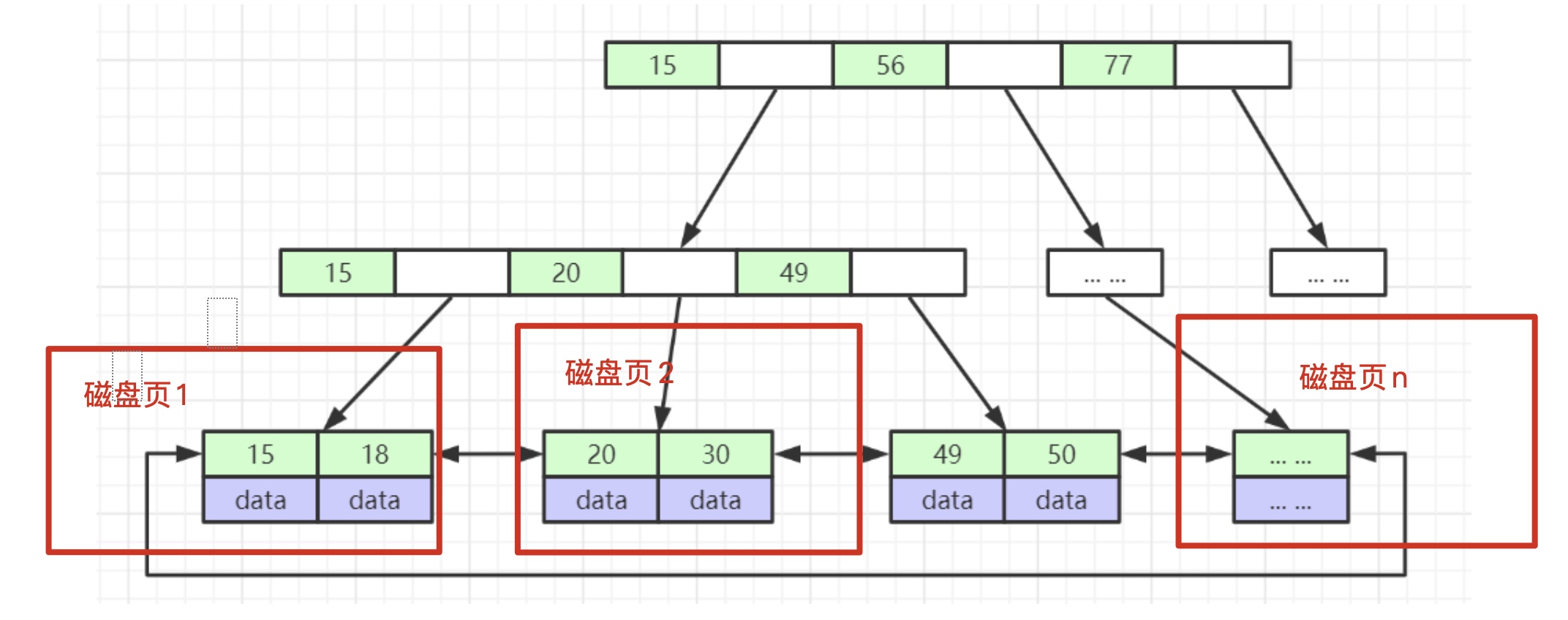
B+Tree

# 数据查询过程

eg: 查询索引值为20的数据

  1. 首先明确一个前提，一个节点就是mysql的一个磁盘页
  2. 首先将第一个节点（磁盘页）的数据load到内存中，通过高效查询算法，比如二分查找算法，快速找到20所在的区间位置是15-56
  3. 通过15找到15-49这个节点，将其load到内存中，再通过高效查询算法，找到20所在的区间位置20-49
  4. 通过20取出磁盘页2，将其load到内存中，在内存中对比，找到20，将叶子节点对应的数据返回

# B+树就解决了红黑树高度不可控的问题吗？

答案是肯定的！

# 一页能存放多少数据

刚才提到了磁盘页，那么我们先来看看一页可以存储多少数据，简单计算一下。

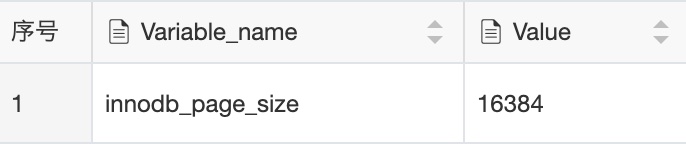
通过下面这条命令查询MySQL一页的空间大小

show VARIABLES like 'InnoDB_page_size'

MySQL默认的值是16384, 也就是16KB(一般情况下，不建议对这个值进行修改) B+Tree

# 为什么是16KB

我们可以简单的计算一下16KB大概可以存放多少索引

首先来看下各类型的存储需求(即占用空间大小)

列类型 存储需求
TINYINT 1个字节
SMALLINT 2个字节
MEDIUMINT 3个字节
INT, INTEGER 4个字节
BIGINT 8个字节
FLOAT(p) 如果0 <= p <= 24为4个字节, 如果25 <= p <= 53为8个字节
FLOAT 4个字节
DOUBLE [PRECISION], item REAL 4个字节
DECIMAL(M,D), NUMERIC(M,D) 变长(0-4个字节)
BIT(M) 大约(M+7)/8个字节

假如有一个bigint的主键，一个bigint占用8个字节，索引后面的磁盘地址大概是6个字节，那么一个磁盘页可以存放多少索引元素 B+Tree

(8 + 6) * n = 16384
n ≈ 1170

也就是说，一个磁盘页可以存放1170个索引，只花了16KB的内存大小

那么叶子节点的磁盘页可以存放多少数据呢？因为叶子节点有一个data元素，这个data可能是索引行的其他列，也可能是索引行数据所在的磁盘空间地址，这与数据库的存储引擎有关，这里先不考虑这个差异。

我们就按存放的是数据来计算，正常一条数据，不会超过1KB，我们按1KB算，那么一个叶节点大概可以存放16个元素（索引大小忽略不计）。

我们可以计算一下，当一个高度为3的B+树被撑满的情况，可以存放多少数据

1170 * 1170 * 16 = 21902400

也就是说，一个千万级别的表，只需要3次文件IO就能拿到数据，查找次数少了几个数量级。

而MySQL的InnoDB引擎早期版本是把根节点的索引常驻内存，高版本（具体是哪个版本，我没有查到）是把非叶子节点都常驻内存的，也就是说，一张千万级的表，最少只需要一次文件IO就能取出数据，那速度自然也就非常快了。

# 一个可能的疑问

一般来说，从内存去查找不耗费什么性能的，更多的时间花在文件IO上。这里你可能会有一个疑问，那既然在内存中查找不耗费什么时间，而且树的高度越低越好，那还要什么索引树， 直接把所有的索引都放在第一个节点，然后把所有的值load到内存中，在内存中比对不就好了？

但这样合适吗？

  1. 可以简单计算一下，还是刚才的例子，一棵高度为3的B+树被撑满的情况下，大概是2000万条数据，一条数据1KB。

    • 使用B+树，一次只需要load16KB的数据在内存中进行查询
    • 不使用B+树呢，一次需要load 2000万KB ≈ 19GB的数据，且不说一张表可能同时可能有很多并发查询，数据库中可能还有好几百张表，这个压力，几百GB的内存的物理机也扛不住，明显是MySQL无法承受之重。

  2. 而且如果把这两千万数据放内存中去对比，不使用任何有序结构，就算是内存中去比较，也不会很快。

# 一个经典问题

现在来回答一个问题，也是一个常见的面试题：为什么MySQL不选择B树要选择B+树作为索引结构呢？

答案其实已经很明显了

因为B树的叶子节点存放了数据

我们还是按一条数据1KB计算，那么一个磁盘页最多能存放16个数据，如果要存放2000万条数据，一个简单的公式如下

16 ^ n = 2000w
n ≈ 6

也就是说，相同的数据量，B+树的构建高度为3的树就可以完成存储，树的高度更低，获取数据所需的文件IO次数更少，查询速度自然也就更快

# Hash索引

  • 对索引的key行一次Hash计算就可以定位出数据存储的位置
  • 很多时候Hash索引要比B+ 树索引更高效
  • 仅能满足 “=”，“IN”，不支持范围查询（工作中一般不使用Hash索引的原因，比如 > 没法查，用不到索引，只能全表扫描）
  • Hash冲突问题

Hash

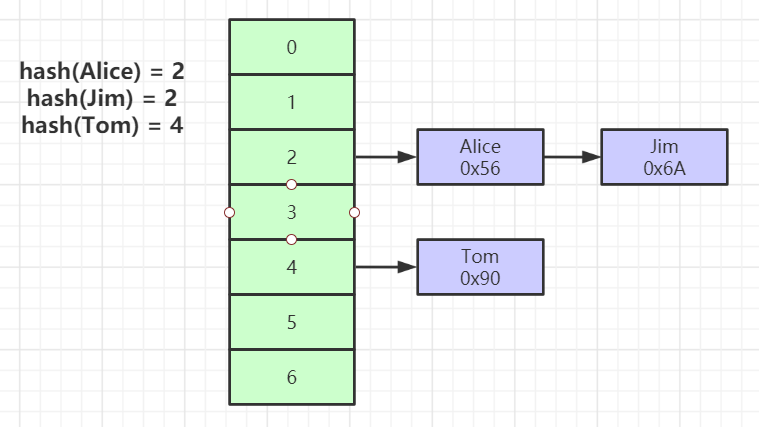
到这里，我们需要回到B+树，看B+树是如何实现范围查询的，这就得提到B+树一个很重要的特性，叶子节点通过指针相连。通过上一条数据可以便捷的找到下一条有序数据， 很好的支持了范围查询。而B树叶子节点并没有指针相连，对于范围查询来说，就很麻烦。

B+Tree

# 存储引擎

# MyISAM存储引擎索引实现

MyISAM索引文件和数据文件是分离的(非聚集)

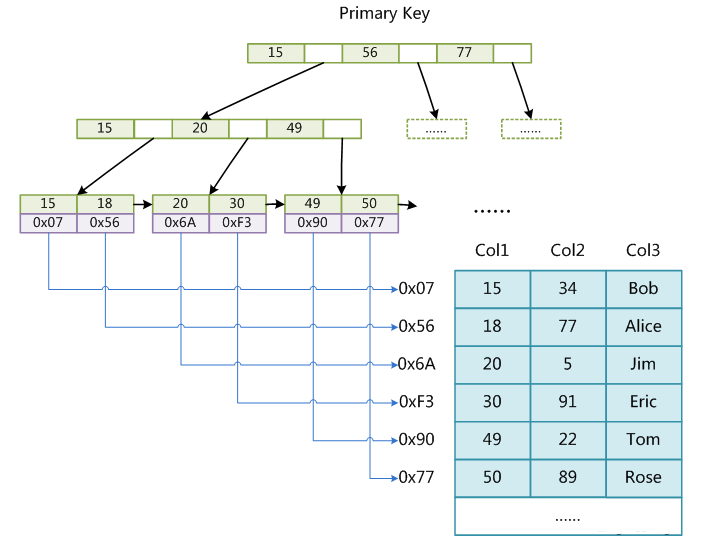
MyISAM

假设我们有一条SQL

select * from t where col1 = 30;

# 查询过程

  1. 按照B+树查询过程，找到col1=30这条索引叶子节点
  2. 根据叶子节点存放的索引行所在的磁盘地址从文件中获取数据

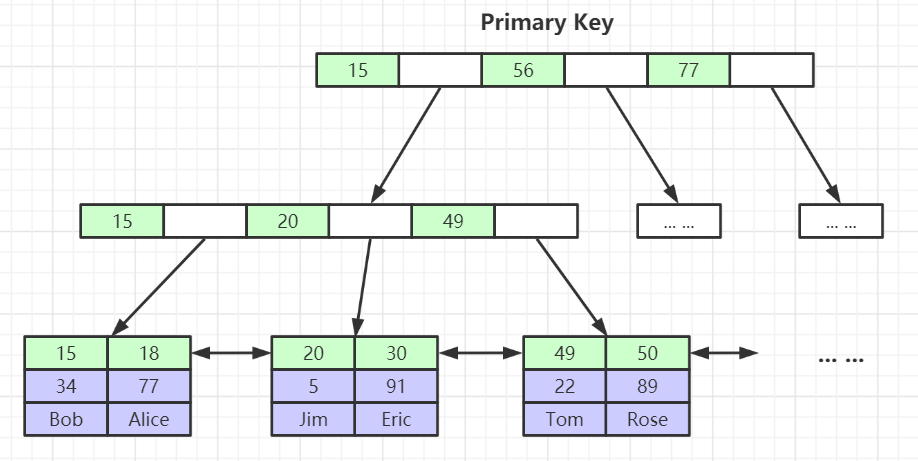
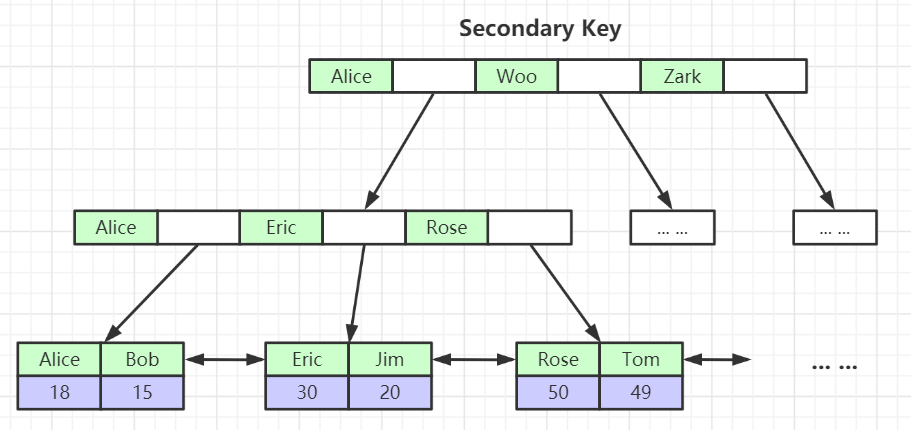
# InnoDB存储引擎索引实现

  • 表数据文件本身就是按B+树组织的一个索引结构文件
  • 聚集索引-叶节点包含了完整的数据记录，这是InnoDB和MyISAM的区别

主键索引 二级索引

# 几个常见的问题

# 聚集索引&聚簇索引&稀疏索引是什么？

  • 聚集索引&聚簇索引

    叶子节点存放整行的数据，InnoDB的主键索引使用该结构

  • 非聚集索引&稀疏索引

    叶子节点存放的是整行数据的文件地址，MyISAM的主键索引使用该结构

# 哪一个查询速度更快？

当然是聚集索引更快，因为从叶子节点就可以直接取到数据，而不用再多一次文件IO读取文件

# 为什么建议InnoDB的表使用整型自增主键

# 为什么需要建主键？

  1. InnoDB的数据引擎，需要使用B+树索引来组织数据
  2. 如果我们没有设置主键，mysql会怎么组织B+树呢？从第一列开始选，选某一个所有数据都不相等的列来组织B+树。如果不存在这一列，就会用一个隐藏列rowid来组织整张表。
  3. 如果由mysql去挑选，那么我们在用数据的时候就不知道这个数据是怎么存的，出现问题，不好排查。且索引如果是无序的，在插入的时候，可能导致裂分解，重新调整索引树，消耗性能。

# 为什么是整型？

  1. 那么为什么是整型呢？可以想象，整型和字符串相比，占用的空间更少，比较的速度更快。

# 为什么要自增？

  1. 如果不是自增的元素，那么在插入数据的时候，需要对树进行调整，很有可能引起页的分裂，无端消耗性能。这一点和我们为什么要主动建主键的原因是一样的。

简单实验一下：B+Tree (opens new window)

# MySQL最左前缀优化原则是为什么？

# 联合索引的底层数据结构

MyISAM主键索引和联合索引的结构一致 MyISAM

InnoDB的联合索引 主键索引 二级索引

为什么InnoDB是这个索引结构？优缺点是什么？

  • 优点
  1. 一致性：如果联合索引存的也是整行数据，那么必然在对数据进行更新的时候，需要同时对主键索引和联合索引进行维护，那么可能存在不一致的问题
  2. 节省空间：联合索引的叶子节点存的是主键，按bigint计算，也就是8个字节的内存空间，按照预估的一条数据是1KB的大小，这个数据空间占用率的差距也是128倍
  • 缺点
  1. 如果需要查询非联合索引和非主键列，需要再通过一次主键索引查询才能取到对应数据（这也是回表的概念），需要多进行两次文件IO。但实际上这两次文件IO，按2000万条数据进行预估，也就load了32KB的数据进行比较，速度是非常快的。和优点进行对比，那一定是利大于弊的。

# 索引最左前缀匹配原理

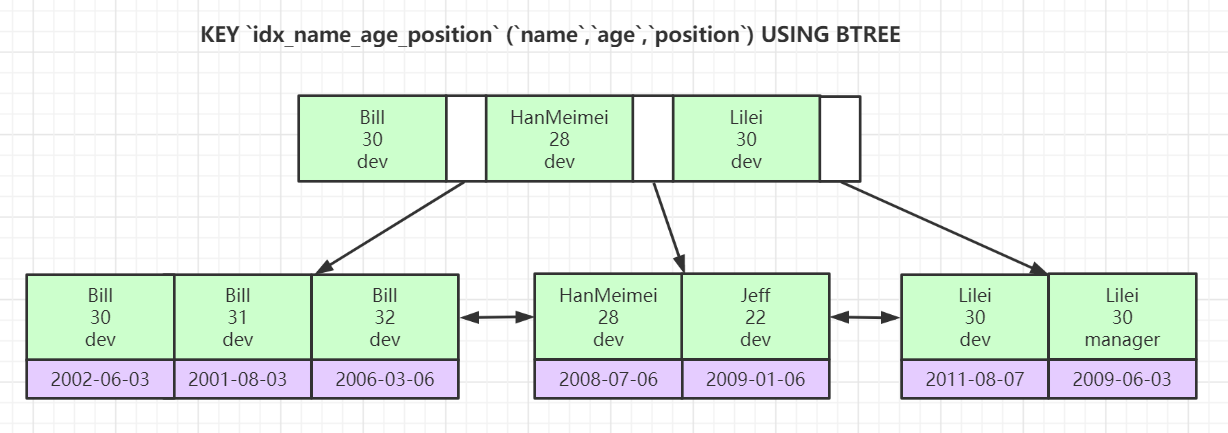
最左前缀匹配原理

# 讨论问题：哪个SQL会走索引？为什么？

select * from t where name = 'Bill' and age = '30';
select * from t where age = 30 and position = 'dev';
select * from t where position = 'dev';

# 说明

  1. SQL1走索引
  2. SQL2不能走索引，跳过了name字段，age和position在索引上无序，只能通过全表扫描才能获取到数据
  3. SQL3不能走索引，跳过了name和age字段，position在索引上无序，只能通过全表扫描才能获取到数据
Last Updated: 12/10/2023, 7:31:44 PM

Explain详解 →